Scripting bettermoments¶
In this Notebook, we will step through how to integrate the moment map making process (in this case, a zeroth moment map, or integrated intensity map), into your workflow. This should elucidate the steps that are taken automatically when using the command line interface.
Standard Imports¶
[1]:
import bettermoments as bm
Load Up the Data¶
Here the load_cube function will return a 3D array for the data and a 1D array of the velocity axis (this should automatically convert any frequency axis to a velocity axis). Note that as we are collapsing along the velocity axis, we have no need for spatial axes, so we do not bother creating them.
[2]:
path = '../../../gofish/docs/user/TWHya_CS_32.fits'
data, velax = bm.load_cube(path)
Spectrally Smooth the Data¶
If you have relatively noisy data, a low level of smoothing along the spectral axis can be useful. bettermoments allows for two different methods: a convolution with a simple top-hat function, or the use of a Savitzky-Golay filter. For a top-hat convolution, you need only specify smooth, which describes the kernel size in the number of channels. For a Savitzky-Golay filter, you must also provide polyorder which describes the
polynomial order which is used for the fitting. Note that smooth must always be larger than polyorder.
It is important to remember that while a small level of smoothing can help with certain aspects of moment map creation, it also distorts the line profile (for example broadening the line in the case of a simple top-hat convolution). Such systematic effects must be considered when analysing the resulting moment maps.
Here we just consider a smoothing with a top-hat kernel that is 3 channels wide.
[3]:
smoothed_data = bm.smooth_data(data=data, smooth=3, polyorder=0)
Estimate the Noise of the Data¶
We require an estimate of the noise of the data for two reasons:
- For the estimation of the uncertainties of the moment maps.
- For applying anything threshold clipping.
To make this estimate, we assume that the noise in the image is constant both spatially (such that the primary beam correction is minimal) and spectrally. To avoid line emission, we consider the RMS of the line-free channels, defined as the first N and last N channels in the data cube.
[4]:
rms = bm.estimate_RMS(data=data, N=5)
Note that the noise estimated this way will differ whether you use the smoothed_data or the original data array. When using the command line interface for bettermoments, the RMS will be estimated on the smoothed data.
[5]:
rms_smoothed = bm.estimate_RMS(data=smoothed_data, N=5)
print('RMS = {:.1f} mJy/beam (original)'.format(rms * 1e3))
print('RMS = {:.1f} mJy/beam (smoothed)'.format(rms_smoothed * 1e3))
RMS = 2.8 mJy/beam (original)
RMS = 2.2 mJy/beam (smoothed)
User-Defined Mask¶
Sometimes you will want to mask particular regions within your PPV cube in order to disentangle various components, for example if you have multiple hyperfine components that you want to distinguish. Often the easiest way to do this is to define a mask elsewhere and apply it to the data you are collapsing (see for example the keplerian_mask.py routine to generate a Keplerian mask).
Through the get_user_mask function, you can load a mask (a 3D array of 1s and 0s) saved as a FITS file, and apply that to the data. If no user_mask_path is provided, then this simply returns an array with the same shape as data filled with 1s.
Note that the user-defined mask must share the same pixel and channel resolution, and be the same shape as the data. No aligning or reshaping is done internally with bettermoments.
[6]:
user_mask = bm.get_user_mask(data=data, user_mask_path=None)
Threshold Mask¶
A threshold mask, or a ‘sigma-clip’, is one of the most common approaches to masking used in moment map creation. The get_threshold_mask provides several features which will help you optimize your threshold masking.
The clip argument takes a tuple of values, clip=(-3.0, 3.0) describing the minimum and maximum SNR of the pixels that will be removed (this is very similar to the excludepix argument in CASA’s immoments task, but with values given in units of sigma, the noise, rather than flux units). clip also accepts just a single value, and will convert that to a symmetric clip as above, for example
clip=(-2.0, 2.0) and clip=2.0 are equivalent. The option to provide a tuple allows the options to have asymmetric clip ranges, for example, clip=(-np.inf, 3.0), to remove all pixels below 3 sigma, including high significance but negative pixels.
It has been found that threshold masks can lead to large artifacts in the resulting moment map if there are large intensity gradients in low SNR regions of the PPV cube. To combate this, users have the option to first smooth the data (only temporarily to generate the threshold mask) which will allow for more conservative contours in the threshold mask. This can be achived by providing the FWHM of the Gaussian kernel used for this spatial smooth as smooth_threshold_mask in number of pixels.
Note that because the data is smoothed, the effective RMS will drop and so the RMS is re-estimated interally on the smoothed image.
Here we mask all pixels with a SNR less than 2 sigma, i.e., 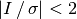 .
.
[7]:
threshold_mask = bm.get_threshold_mask(data=data,
clip=2.0,
smooth_threshold_mask=0.0)
Channel Mask¶
For many PPV cubes, the line emission of interest only spans a small range of velocity axis. This region can be easily selected using the firstchannel and lastchannel arguments in get_channel_mask. Note that the lastchannel argument also accepts negative values, following the standard Python indexing convention, i.e., lastchannel=-1 results in the final channel being the last.
get_channel_mask also accepts a user_mask argument, which is an array the same size as the velocity axis of the data, specifying which channels to include. This may be useful if you want to integrate over several hyperfine components while excluding the line-free regions between them.
[8]:
channel_mask = bm.get_channel_mask(data=data,
firstchannel=0,
lastchannel=-1)
Mask Combination¶
All the masks can be easily combined, either with AND or OR, with the get_combined_mask function. This can then be applied to the data used for the moment map creation through a simple multiplication. Note for all collapse functions, pixels with a 0 value will be ignored.
[9]:
mask = bm.get_combined_mask(user_mask=user_mask,
threshold_mask=threshold_mask,
channel_mask=channel_mask,
combine='and')
masked_data = smoothed_data * mask
Collapse the Data¶
Now that we have a smoothed and masked dataset, we can collapse it along the velocity axis through several different methods. (https://bettermoments.readthedocs.io/en/latest/user/collapse_cube.html#). In general, most functions require the velocity axis, velax, the masked data data, data, and the RMS of the data, rms. The available functions can be checked through the available_collapse_methods function such that the desired function is collapse_{methodname}.
[10]:
bm.available_collapse_methods()
Available methods are:
zeroth (integrated intensity)
first (intensity weighted average velocity)
second (intensity weighted velocity dispersion)
eighth (peak intensity)
ninth (velocity channel of peak intensity)
maximum (both collapse_eighth and collapse_ninth)
quadratic (quadratic fit to peak intensity)
width (effective width for a Gaussian profile)
gaussian (gaussian fit)
gaussthick (gaussian with optically thick core fit)
gausshermite (gaussian-hermite expansion fit)
Call the function with `collapse_{method_name}`.
Each function will return moments, an (N, Y, X) shaped array, where (Y, X) is the shape of a single channel of the data and N is twice the number of statistics (with the uncertainty of each value interleaved). To see which parameters are returned for each collapse_method, we can use the collapse_method_products function. For the 'zeroth' method:
[11]:
bm.collapse_method_products('zeroth')
[11]:
'M0, dM0'
So we have the zeroth moment, M0, and it’s associated uncertainty dM0.
Here we will collapse the cube to a zeroth (integrated intensity) map.
[12]:
moments = bm.collapse_zeroth(velax=velax, data=masked_data, rms=rms)
Save the Data to FITS¶
It’s possible to work with the data directly, however it’s often useful to save these for later. The save_to_FITS function will split up the moments array and save each one as a new FITS file, replacing the .fits exention with _{moment_name}.fits for easy identification. The header will be copied from the original file.
[13]:
bm.save_to_FITS(moments=moments, method='zeroth', path=path)